Physicism!!!
I heard that on the quiz/test, whatever it is, it's gonna be an object shot straight horizontally, so here's a practice sheet he gave us of such a problem.
Hurting your eyes? Eye-friendly copy?
CITY LIFE SHEET
Two apartment buildings, each 45 high with level roofs, stand exactly 60 meters apart.
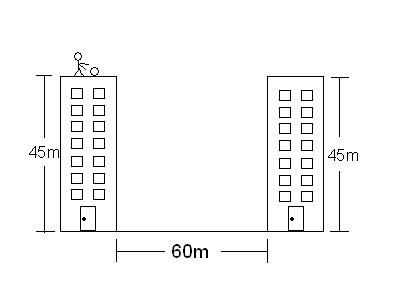
1. A girl on the roof of one building rolls a bowling ball off the top of the building, towards the other. What is the greatest speed the bowling ball can have to insure it hits the ground below, and not the other building?
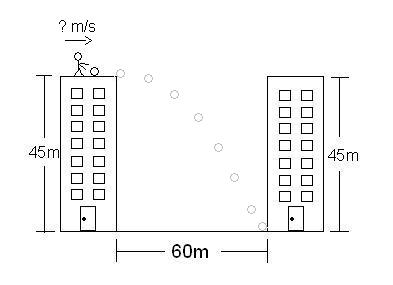
What you want to find first is the time that the object will hit the ground. First you want disregard that the bowling ball has a velocity goin sideways (even though that's what we find at the end) and pretend that it is being dropped normally as if in those free fall problems. Therefore, you use the following equation:
(delta)Y = V(original)T + (.5)GT^2
When we plug in the numbers, the equation is this:
-45m = (0m/s)T + (.5)(-10m/s/s)T^2
-45m = (-5m/s/s)T^2
9ss = T^2
3s = T
We use negative 45 because the bowling ball starts at "0" and goes 45 meters downwards. The initial velocity is zero because this is the initial velocity of Y, and since she didn't apply any force upwards or downwards to the ball (force was applied sideways, so doesn't affect Y), then that would mean that it started with zero velocity.
Now that you have time, you can find out what the velocity she threw the ball at is. The time you found is the time the ball will reach the ground, no matter how fast she throws it. But, since the distance between the buildings is 60 meters, and that's the distance you want the ball to touch the ground, we can plug in the time and the meters to the X displacement equation:
(delta)X = V(original)T + (.5)AT^2
Once we plug in the numbers you'll get this:
60m = V(original)(3s) + (.5)(0m/s/s)(3s)^2
60m = V(original)(3s)
20m/s = V(original)
And thus you found the original velocity or speed that she threw the ball at, w00t.
2. Suppose she rolls the ball with a speed of 40m/s. It will strike the other building at what distance above the ground?
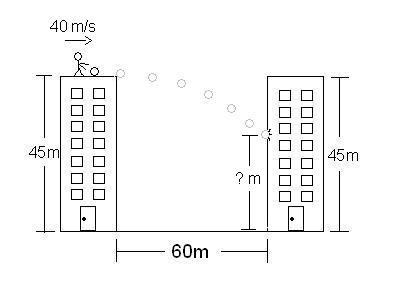
Now, this is similar to the question in number one, the only difference here is that instead of the ball going 45 meters down and 60 meters accross, it goes X meters down and 60 meters accross, but we're given the original velocity, so in other words, we work backwords from the way we did at number 1.
So first, as almost always, we want to find the time first. Only here, instead of finding the time the ball strucks the floor, we find the time the ball crosses 60 meters. Thus, we use the equation (delta)X = V(original)T + (.5)(A)T^2.
So when we plug in the numbers we get:
60m = (40m/s)T + (.5)(0m/s/s)T^2
60m = (40m/s)T
1.5s = T
Since there's no acceleration in the right or left movement (the ball is always going 40m/s to the right throughout the whole trip), the second part of the equation is canceled, leaving only the first part, and finding out that the ball travels the 60 meters in 1.5 seconds. Now that we have the time, we can find out at what height change it undergoes. So we take the time and plug it in to the displacement equation for Y. However, this time you want the final position, which is seperate from the displacement, so we just break up (delta)Y into Y(final) - Y(original), Y(original) being 45 meters high.
(delta)Y = V(original)T + (.5)GT^2
Once we plug in:
Y(final) - 45m = (0m/s)T + (.5)(-10m/s/s)(1.5)^2
Y(final) = (-5m/s/s)(2.25ss) + 45m
Y(final) = 33.75m
Therefore, the bowling ball will strike the building at 33.75 meters. Another possible way of doing this is finding the displacement, which would be -11.25. In that case, you'd have to use common sense and realize that you're 45 meters up, and if you go -11.25 meters, that'd be 11.25 meters down, so you substract and get the same answer. Caution, you cannot use this second method of doing it if the problem involves angles, ONLY if the object is shot horizontally. Major w00tness.
3. What speed must she choose if she wants the ball to enter a window of the other building which is 25 meters above the ground?
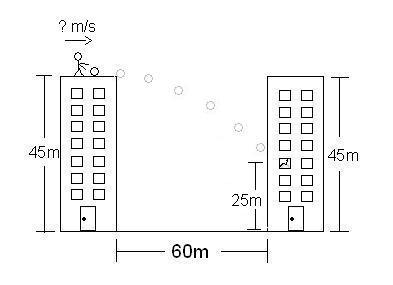
This little baby is a trickster, actually, I'm kidding, it's easy as taking a huge dump, and as rewarding too. Ok, You have Y displacement (45 - 25 = 20), and you need to find the velocity she throws it again. In this case, the problem is exactly the same as number one, only that instead of -45 for displacement, you use -20, because it goes 20 meters down from your original position. So first, as said on number one, we find the time with the Y displacement equation.
(delta)Y = V(original)T + (.5)GT^2
And when we plug in:
-20m = (0m/s)T + (.5)(-10m/s/s)T^2
-20m = (-5m/s/s)T^2
4ss = T^2
2s = T
Look at that, ain't it purdy? Let's plug that biatch to the X displacement equation to find out the original velocity (velocity she fired the ball at).
(delta)X = V(original)T + (.5)AT^2
And once we plug in:
60m = V(original)(2s) + (.5)(0m/s/s)(2s)^2
60m = V(original)(2s)
30m/s = V(original)
OMFG! Is that what I think it is? Yes, it's the answer! Congratulation, you're now a 1337 Physicist!
Wanna Prove Your 1337ness?
DIVE BOMBER SHEET (Extra Practice)
An American dive bomber delivers its bombs by merely dropping them (not firing them) out of the plane. Thus the bombs, upon release, have exactly the same velocity as the plane.
Your mission: Fuck those Nazis sons of bitches.
1. The bomber, flying level (straight to the horizon, ie parallel to ground), at an altitude of 1000 meters, spots a Nazi tank at rest. The plane has a speed of 100m/s. From what horizontal distance from the tank must it release its bomb in order to make a hit?
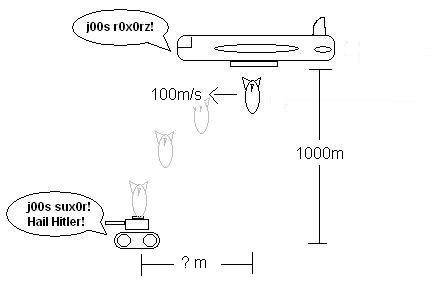
Let's see now. Yes, yes, yes, mmmm, yes, yes, I've got it! Ok, Since the plane is moving exactly horizontal, we can assume that its velocity is also the horizontal, or X, velocity of the bomb. Therefore, the bomb's X velocity is 100m/s. Now, to find out the distance from where the plane should release the bomb, or the X displacement, we need to find how long it'll take the bomb to reach the ground. In that case, since the bomb was released, and not fired, it's original Y velocity is zero, and since it has to go 1000 meters to reach the ground (-1000), we can use the Y displacement equation to find out the time like so:
(delta)Y = V(original)T + (.5)GT^2
With the numbers plugged in:
-1000m = (0m/s)T + (.5)(-10m/s/s)T^2
-1000m = (-5m/s/s)T^2
200m = T^2
10*sqrt[2]s = T
Now that we have the value of T, square root of 200 or ten times the square root of two, we plug that in on the X displacement equation.
(delta)X = V(original)T + (.5)AT^2
And once we plug in:
(delta)X = (100m/s)(10*sqrt[2]s) + (.5)(0m/s/s)^2
(delta)X = (100m/s)(10*sqrt[2]s)
(delta)X = 1414m
And there's your answer to number one. The bomber has to release his bomb 1414 meters away from the tank to make a successful Nazi kill.
2. Assume that the conditions of problem 1 prevail, but the bomber is diving at 30 degrees below horizontal.
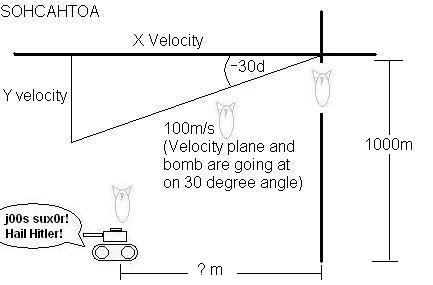
Now this is were it really does get tricky. The plane is diving at a 30 degree angle below the horizon, in a cartitian plane, 330 degrees or 210.
Since the 30 degrees is below the horizon, they are negative. Now, to find out the horizontal and vertical velocities, we must use sin and cosin. Remember SOHCAHTOA, sin = Opposite side of angle/Hypotneus, cosin = Adjacent side of angle/Hypotneus, and tangent = Opposite side of angle/Adjacent side of angle. With this knowledge, we use cosin to find the Y velocity and sin to find the Y velocity.
Y velocity = 100m/s*cosin(-30)
Y velocity = -50m/s
X velocity = 100m/s*sin(-30)
X velocity = 86.6m/s
You may be concerned that the Y velocity is negative, and that's ok, some people are dumb like that. The Y velocity is negative because the plane is diving downwards, and down is a negative quantaty. Anyways, now that we have the X velocity and the Y velocity, we can go about the problem as we did for number 1, only this time, we have an original velocity for Y, so we'll have to use the full equation. First we find the time it'll take the bomb to go the 1000 meters downwards.
(delta)Y = V(original)T + (.5)GT^2
With the numbers plugged in:
-1000m = (-50m/s)T + (.5)(-10m/s/s)T^2
-1000m = (-50m/s)T + (-5m/s/s)T^2
5m/s/sT^2 + 50m/sT - 1000m = 0
T^2 + 10T - 200 = 0
Using the quadratic equation, we get 10 and -20. -20 is quickly discarded because you can't have a negative time, so we're left with 10, meaning it takes 10 seconds for the bomb to hit ground. Taking this informating, we plug in the numbers on the X displacement equation to find out how far from the tank the bomb must be released.
(delta)X = V(original)T + (.5)AT^2
And once we plug in:
(delta)X = (86.6m/s)(10s) + (.5)(0m/s/s)(10s)^2
(delta)X = (86.6m/s)(10s)
(delta)X = 866m
And there's your answer. I know what you're thinking. Why could we cancel out half of the equation here, but not when we looked for time? Well, the point being that the plane's velocity is what affects the X velocity, using cosin we found out it was 86.6. But other than that, there is no other force affecting X, meaning there is still no acceleration, and thus, half the equation can be canceled. Half of the Y equation could be canceled before because the bomb was just being dropped, so there was no original velocity, therefore canceling that part of the equation. However, since the plane is in a dive, the bomb now has a velocity, and with the constant force of gravity, it has an acceleration too. Therefore, you had to do that tiny bit of more work that one bitches about so much and use the quadratic equation to find out what time is. :) On to #3...
3. Suppose the plane is flying level (at 1000m), but the tank is moving with a constant speed of 10m/s, in the same direction as the plane. At what horizontal distance from the tank must the plane release its bomb to score a hit?
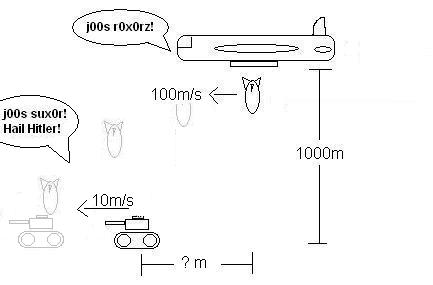
Ok, first, you want to ignore that little tid bit of the tank, and concentrate about when the bomb is going to hit the ground, as we did on number one. If you look at number one, you'll see that the bomb will hit the ground at 10*sqrt[2] seconds. Now that you have found that out, we can go on to worry about those damn Nazi's and their trickery.
Since 10*sqrt[2] seconds will pass after the bomb will be released before it hits the tank, the tank will have moved. So the point here, is to make sure that both the bomb, and the tank's final position are equal. To do that we use the X displacement equations for both of them, changing X displacement to X(final) - X(original) and adding x(original) to both sides, like so:
X(final) - X(original) = V(original)T + (.5)AT^2
X(final) = X(original) + V(original)T + (.5)AT^2
Plug in the numbers for both the tank and the bomb, and then set them equal to eachother to find out at what distance the plane should throw the bomb to kick some Nazi ass.
X(final-t) = X(original) + (10m/s)(10*sqrt[2]s) + (.5)(0m/s/s)(10*sqrt[2]s)^2
X(final-t) = X(original) + (10m/s)(10*sqrt[2]s)
X(final-b) = 0m + (100m/s)(10*sqrt[2]s) + (.5)(0m/s/s)(10*sqrt[2]s)^2
X(final-b) = (100m/s)(10*sqrt[2]s)
Now set them equal to eachother:
X(original) + (10m/s)(10*sqrt[2]s) = (100m/s)(10*sqrt[2]s)
X(original) = (100m/s)(10*sqrt[2]s) - (10m/s)(10*sqrt[2]s)
X(original) = 1414.2 - 141.4 = 1272.8m
And thus the plane will have to be 1272 meters from the tank when dropping the bomb to hit it. I know this one is a little confusing. The "0m" on the displacement equation for the bomb is 0m because we assume that the point where the bomb is dropped is zero meters. Now, you might think, "Hey, that's just finding the tank's original position!" No shit, if the point where the bombs are released is zero, then how many feet the tank is located at that original point will be the distance. Anyways, this is one's a little hard to explain on text, so if anyone doesn't understand it, just find me tomorrow and we'll talk about it. Anyways...
4. Suppose the tank is moving as in problem 3 but the plane is in a dive of 30 degrees to the horizontal. What must be the horizontal distance in this case?
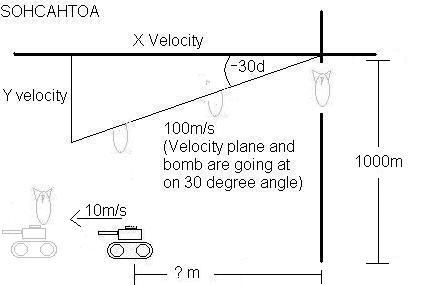
This is pretty much number 2 and number three combined, so to save me a shit load of time, I'm just gonna copy excerpts from both and stick em in here, enjoy.
Ok, first, you want to ignore that little tid bit of the tank, and concentrate about when the bomb is going to hit the ground, as we did on number two. Using sin and cosin you'll find out that the bomb will hit the ground at 10 seconds. Now that you have found that out, we can go on to worry about those damn Nazi's and their trickery.
Since 10 seconds will pass after the bomb will be released before it hits the tank, the tank will have moved. So the point here, is to make sure that both the bomb, and the tank's final position are equal. To do that we use the X displacement equations for both of them, changing X displacement to X(final) - X(original) and adding x(original) to both sides, like so:
X(final) - X(original) = V(original)T + (.5)AT^2
X(final) = X(original) + V(original)T + (.5)AT^2
Plug in the numbers for both the tank and the bomb, and then set them equal to eachother to find out at what distance the plane should throw the bomb to kick some Nazi ass.
X(final-t) = X(original) + (10m/s)(10s) + (.5)(0m/s/s)(10s)^2
X(final-t) = X(original) + (10m/s)(10s)
X(final-b) = 0m + (86.6m/s)(10s) + (.5)(0m/s/s)(10s)^2
X(final-b) = (86.6m/s)(10s)
Now set them equal to eachother:
X(original) + (10m/s)(10s) = (86.6m/s)(10s)
X(original) = (86.6m/s)(10s) - (10m/s)(10s)
X(original) = 866m - 100m = 766m
And thus the plane will have to be 766 meters from the tank when dropping the bomb to hit it. I know this one is a little confusing. The "0m" on the displacement equation for the bomb is 0m because we assume that the point where the bomb is dropped is zero meters. Now, you might think, "Hey, that's just finding the tank's original position!" No shit, if the point where the bombs are released is zero, then how many feet the tank is located at that original point will be the distance. Anyways, this is one's a little hard to explain on text, so if anyone doesn't understand it, just find me tomorrow and we'll talk about it.
.....Brown Power!

